لا تنسَ أنّ العد للمليون يستغرق وقتاً كبيراً جداً والعد للمليار يحتاج عقوداً طويلةً، ولو أردنا ترك هذا الحساء لمليارات السنين لن يكفيه، ولو امتلكنا مليارات المليارات من الحاسبات الذكية بسرعات مذهلة موجودة لتحاكي تفاعل المواد في حوض الماء هذا، فلن يكفيها عمر الكون لإنتاج بروتين واحد بالاحتمالات العشوائية.
ولنتمكن من تخيّل استحالة هذه الأرقام، لنبيّن الأمر باستخدام ما في أيدي البشر من إمكانيات فجهاز حاسب يحتوي معالج CPU يعمل بسرعة 3 جيجا هرتز أي 3 مليار نبضة في الثانية، يحتاج إلى نحو 126 مليون مليون سنة لمُجرَّد العد من صفر إلى 10^30، أي أنّ هذا الحاسب لكي يعد إلى الاحتمال ذو 800 صفر، فإننا يجب أن نضع على يمين الزمن 126 مليون مليون سنة، أي 770 صفراً أخرى، مرة أخرى هذا فقط مع أننا فرضنا شرطين فقط، ولم نفرض باقي الشروط لأنّ الأرقام لن يتحملها الدماغ حينما نفكر بها، المُشكِلة أنّ الأرقام هنا تفقد معناها، ولو كنت مبرمجاً للُغة برمجة ما، ستعلم أنّ كتابة الشيفرة البرمجية (الكود) لبرنامج يعد الوقت المطلوب لإجراء أي احتمالات لا يتعدى 5 أسطر برمجية، إذ تحسب الوقت لكي يعد جهازك لـ10^10 وذلك بطرح وقت بدء العد بوقت نهاية العد، وبعد ذلك تضرب الرقم في 10^790، وهو أمر لا يستطيع فعله حاسوبك ولا أي حاسوب في العالم، جرب أن تضرب الرقم في 10^20 بدلاً من ذلك وستجد أن 10^30 مثلاً هو وقت فوق ال100 مليون مليون سنة، وهو رقم أكبر بكثير من عمر الكون وليس الكرة الأرضية فحسب، فعمر الكون 13.8 مليار سنة وهذا رقم صغير مقارنة باحتمالية العد من 10^30، فما بالكم ب10^800 لتصنيع بروتين واحد في بيئة مُعدّة له، وما بالكم بتصنيع باقي البروتينات وأجزاء الخلية، لاحظ أننا نتكلم هنا عن برنامج يجعل الحاسوب يعد عداً ولا يُجري تجارباً، نحن نتحدث عن برنامج عداد يضرب الأرقام فقط، أرقاماً أقل من الرقم 10^30، حقيقة بصفتي مبرمجاً أستسلم وأُسلّم بوجود قوة عظمى جداً فوق هذه الاحتمالات فلا مجال إلا لذلك.
في الحقيقة هذه الفكرة يؤمن بها كل الماديين الذين شاهدتهم، إلا مُحبّي البوب سينس والتيك أواي الذين شاهدوا عدداً من المقاطع على اليوتيوب مُعتقدين أنّ نشوء الخلية الأولى بالصدفة في إناء به بعض الحساء أمراً ممكناً حسب تجربة يوري ميلر، إذا استمعت لكارل ساجان أو لريتشارد دوكينز فسترى أنهم يعرفون صعوبة وجود الخلية الأولى من العدم بمحض الصدفة، وهم يعزون وجودها إلى مخلوقات ذكية أتت من كوكب آخر، سبحان المصممين الأوائل، سبحان المخلوقات الذكية التي ممكن أن تكون أي شيء إلا أن تكون الله، في الحقيقة أحترم العُلماء الذين يقولون أنه من الصعب وجود الخلية بالصدفة، وينتقلون إلى الحديث عن التطور بعد الخلية الأولى وليس قبلها، وكل ما يجري لمحاولات تفسير الحياة الأولى على الأرض هو محاولات فقط لتوضيح مقتطفات من عمليات الخلية وليست حبكة كاملة بعد، لو أردنا الحديث عن بروتينات أكبر قليلاً فالموضوع يأخذنا إلى أرقام مخيفة أكثر.
هذا يقودنا إلى فكرة أنّ العُلماء يؤمنوا قبل أن يكتشفوا، فحينما نرى أنّ الأرقام تقول أنه لا يمكن إلا أن يكون هُنَاك قوة فوق هذه الاحتمالات، ويؤكد العُلماء أنه من غير الممكن مستقبلاً أن نكتشف شيئاً آخراً ساعد الصدفة، فنحن هنا ندخل في مرحلة الإيمان كما الأديان، العُلماء مُؤمِنون بوجود حجاب سيُكشف عنه مستقبلاً، وهذا ما يؤمن به المُؤمِنون أنفسهم، فهُنَاك في المستقبل توضيحات ومكاشفات من الإله لهم في الدنيا والآخرة، وعلى هؤلاء العُلماء المُؤمِنين أن يتخلوا عن العلم، فالعلم يعترف بالموجود ولا يعترف بالإيمان، وحينما يؤمن العُلماء نستطيع أن نقول أنهم والمُؤمِنون سواء، فهذا العالِم يؤمن بوجود قوة سيتم الكشف عنها مستقبلاً ولا يتقبل الحقائق التي بين يديه، والمُؤمِن يؤمن بوجود قوة خارقة ستكشف عن نفسها بطرقٍ شتى وصولاً إلى يوم الحساب ولا يتقبل بوجود خالق غيرها، في كل الأحوال هذه الأرقام تدفعني إلى أن أفكر بوجود قوة عاقلة يجب البحث عنها.
|
رابط 9 مقطع يوضح تكون الدنا من البروتين |
ولنفرض جدلاً بطريقة ما قد تكون بروتين في وسط بحيرة ماء من حساء الحياة، نحن نعرف أنّ قوانين الديناميكا الحرارية وخصوصاً القانون الثاني الذي عرضناه في الفصل الأول يحيلنا للتفكير إلى أنّ محيط البروتين المتكون مليء بالكثير من الإنتروبيا وبهذا سيتفكك البروتين وسيتكسر، إذن الخيار الأمثل هو أن يرجع خطوة للخلف وألا يتقدم للأمام، فنحن حينما نضع سيارة في الصحراء لا نتوقع بسبب العوامل المحيطة أن تتحول إلى طائرة، وما نجده بعد أشهر من تركها أنّ عجلها قد نقص منه الهواء، وزجاجها أمسى مخدوشاً من دفع الرمال، وطلاؤها قد تساقط من الأكسدة، ومحركها قد تلف وغيرها من الأمثلة، وفي الأحياء سيكون القانون نفسه، فالبروتين الأول أو حتى الخلية الأولى لو بقيت في وسطها ستتحلل وتموت لأنّ جميع العوامل حولها ستحاول قتلها وليس دفعها للأمام، فأين من يفسر هذه النقطة ويوضحها!
احتمال رسم الموناليزا
وبصفتي أعمل مُبرمِجاً منذ سنوات طويلة، أتفهم موضوع الاحتمالات وقدرات الحاسوب والتوليد العشوائي بشكل كبير، لذلك في هذا الفصل الجميل المقتبس من فصل أبدع حاسب وأبدع نظام تشغيل للمهندس محمد غانم، سنحاول أنّ نتفهم الأرقام الكبيرة التي ظهرت لنا فوق وذلك بالمنطق والماوس والكيبورد.
لنفترض أنّنا نريد كتابة برنامج بسيط يحاول أن يرسم الموناليزا عشوائياً، ولنأخذ شاشة حاسب بأقل دقة ممكنة حتى نجري تجربتنا، وأقل دقة شاشة يمكن أن نجرب عليها هي دقة فيها 480 × 640 نقطة، أي أنّ هذه الشاشة تحتوي على 307200 نقطة، البرنامج سيقوم بتوليد كل النقاط عشوائياً وحتماً ستكون إحدى التوليدات هي صورة الموناليزا.
صورة الموناليزا ملونة كما نعلم ورسمها سيكلف الكثير من الاحتمالات، لذلك سنخفض الألوان إلى 256 لوناً بدلاً من ملايين الألوان، اممم! دعنا نبسطها أكثر، لنبقيها على 16 لون حتى تنجح التجربة، أتعلمون سنكتفي بالأبيض والأسود فقط لتبسيط الأرقام، جيد! نريد خياراً أبسط، لأنّ أي خيار آخر ستنتج عنه أرقام مزعجة.
ما بين أن تكون كل نقاط الشاشة بيضاء، أو أن تكون كلها سوداء، فإن عدد من التباديل يساوي عدد الأرقام الثنائية التي يمكن وضعها في 307200 خانة، أي أنّ الاحتمالات المتاحة هي 2^307200 = 1092000^ احتمال وهي أكثر بكثير من الاحتمالات التي استعرضناها من مجموع كل احتمالات الكتاب للآن.
لو نجحنا في تجربة كلّ هذه الاحتمالات، فسنحصل بالأبيض والأسود على جميع اللوحات التي رُسمت أو لم ترسم بعد، وعلى كل صور الأشياء والأشخاص التي نتخيلها أو لم نتخيلها، وستظهر حتماً لوحة لمونيكا بيلوتشي مع ريناتو، هذا الكلام جميل وبسيط، لكن المُشكِلة تكمن في أنّ تجربة هذه الاحتمالات يحتاج إلى عمر يفوق عمر الكون بمليارات مليارات المرات، كيف ذلك؟ إليك التوضيح.
لنفترض أنّ لدينا حاسباً يستطيع رسم كل احتمال من هذه الاحتمالات في جزء من مليار جزء من الثانية وهذا أمر مُستحيل عملياً بأجهزة اليوم لكن سنفترضه، هذا يعني أنه يستطيع أن يرسم في عام واحد:
مليار × 60 ثانية × 60 دقيقة × 24 ساعة × 365 يوم = 22118400 مليار لوحة في العام، وهو ما يساوي تقريباً: 1018^.
وهذا يعني أننا نحتاج لكي نرسم كلّ اللوحات الممكنة، إلى عدد من الأعوام يساوي: 10^92000 تقسيم 10^18، أنت تعرف من الرياضيات أنّ قسمة الأسس تتم عبر طرح الأسس، وفي الواقع طرح العدد 18 من 92 ألفا سيعطينا رقم لا يبتعد كثيراً عن سابقيه.
دعنا نفترض أنّنا نستخدم مليار حاسب (10 أس 9) في تجربتنا، هذا سيعطينا (10^18) × (10^9) = 10^27 لوحة في العام، أعلم أعلم لا يزال الرقم تافهاً.
دعنا نفترض أنّ هُنَاك مليار كوكب مثل الأرض على كلّ منها مليار حاسب تشارك في العملية، هذا سيرفع العدد إلى (10^36) لوحة في العام، لا تقلق فأنا أعلم أنّ الرقم لا يزال غير مجدياً!
هذا يعني أننا نحتاج في سبيل رسم كل اللوحات إلى زمن يساوي 10^(92 ألفا – 36) من السنوات، أي نحو مليار مضروباً في نفسه 10 آلاف مرّة من السنوات، أعلم أنّ الرقم خرج من دماغك وأنك تخاف من هذا التفكير لذلك قرأته مسرعاً، لذلك نحن بحاجة إلى إعادة تبسيط الأمور، لنكسر الشاشة ذات الأبعاد 480 × 640، ولنستخدم شاشة دقتها 80 × 80 نقطة فقط، هذا سيجعلنا ننتظر 10^2000 من السنوات، أوبااا، ما زلنا لا نفهم الأرقام المرعبة هذه، إذن فلنقلص الشاشة إلى: 20 × 20 نقطة، أي نحو 5% فقط من أبعاد شاشة الحاسب الأولى القديمة، أي شاشة قطرها أقل من بوصة، هذا غير كافٍ لرسم لوحة واضحة المعالم والتفاصيل، لكن نتجاوز الأمر، وهذا يعني 2^400 = 10^120، وهذا ما يحتاج إلى أكثر من (10^80) عاماً لتجربتها، أي مليار مليار مليار مليار مليار مليار مليار مليار مليار سنة.
سنفترض أنّ لكل لوحة مليار نسخة مقاربة ناتجة عن اختلاف مواضع بعض النقاط، إذ يمكن مطابقتها بالصورة الحقيقية لكن باختلافات طفيفة، هذا مُستحيل مع لوحة حجمها 20×20 نقطة لكن لأجل الأخوّة سنتجاوز، هذا لن يغير شيء يُذكر في الأرقام السابقة، سننتظر 10^71 عاماً، بدلاً من 10^80 عام.
|
رابط 10 فيديو توضيحي لشرح النظام |
رابط التحميل |
تكرم، مرة خامسة لأجل عيون مونيكا، لنكن كرماء، ونفترض أنّ لكل لوحة مليار مليار احتمال، هذا سيجعلنا ننتظر 10^62 عام، أنت لا تصدق هذا الكلام، حسناً لا مُشكِلة، هاك الرابط بالأسفل به الشيفرة البرمجية لتجربة الأمر بنفسك.
لو قمنا بتشغيل هذا البرنامج العشوائي لرسم اللوحات بافتراض أنه لن يكرر أي لوحة -وهذا لن يحدث في الواقع- فما هو احتمال أن نحصل على اللوحات الموجودة في متحف اللوفر، أو حتى على لوحة الموناليزا فقط؟ لو جربت البرنامج السابق، فلن تحصل إلا على فوضى من النقاط البيضاء والسوداء.
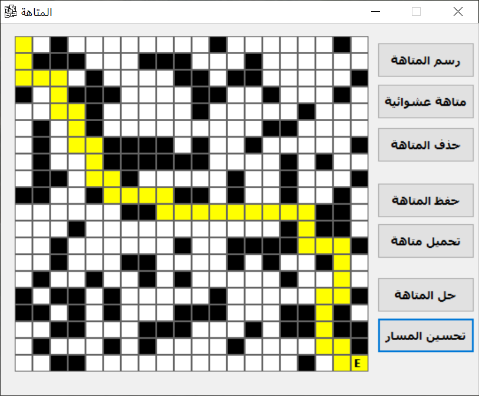
يمثل (شكل 30 برنامج المتاهة) برنامج اسمه Maze يحاول حل متاهة تتكون من ٢٠×٢٠ خانة، عند الضغط على زر “متاهة عشوائية” سيرسم البرنامج الصورة الصغيرة التي تكلمنا عنها هنا وذلك بتلوين الخانات عشوائيا بالأبيض والأسود، حاول أن تجرب إلى أن تمل، وانظر هل ستحصل على كلمات أو على صور لها معنى أم لا، لا تنسَ أن تلاحظ أننا تحكمنا في عشوائية الأبيض والأسود، فقد تكون النقاط السوداء أقل من ثلث النقاط البيضاء، ليجد الإنسان الآلي طرقاً يمشي فيها لأنّ البرنامج يعتبر الخانة السوداء عائقاً، أيضاً لاحظ أنك لا تستطيع فعلياً كتابة البرنامج الذي يحفظ الصور العشوائية في ملفات، لأنك لو فعلت هذا فستستهلك كل مساحة القرص الصلب قبل أن تحصي من الاحتمالات عدداً ملموساً.
وماذا لو علمت أنّ عدد أنواع الأحياء على سطح الأرض يقدر بنحو 4.5 مليون نوع، فما هو احتمال أن نحصل على لوحات ثنائية البعد من اللونين الأبيض والأسود لأيّ من هذه الأحياء عبر برنامجنا للرسم العشوائي!
هذا الاحتمال سيساوي 4.5 مليون من (10 ^120) أي 1 من (10^113).
دعنا نفترض أنّ لكل لوحة مليار مليار نسخة مقاربة، أي أنّ الاحتمال سيكون 1 من (10^96)، وإنّ كمية الاستحالات التي توضحها لنا الأرقام يظهر عبثية التفكير في خيار الاحتمالات عبر الصدفة، هذا ونحن نتكلم عن لوحة بحجم صغير 20 نقطة × 20 نقطة وثنائية البعد أي مسطحة بلونين فقط هما الأبيض والأسود، فما بالنا عندما نتكلم عن مجسمات ثلاثية البعد، وما بالنا لو لم تكن هذه المجسمات مُجرَّد رسوم، بل كائنات حية من لحم ودم تحمل تركيباً تقنياً مُعقَّداً، يستغرق الكلام عنه آلاف المجلدات من حصيلة بحوث العُلماء عبر القرون.
لعلك تعلم أنّ الكائنات الحية يمكن تشبيهها بالبرامج التشغيلية في الحاسوب فالجينوم الخاص بها يشابه عدد أسطر الشيفرات البرمجية، هذا لو افترضنا أنّ شيفرة الدنا كافية في بناء نظام الإنسان الكامل، وما استعرضناه يبين أنها غير كافية، ولكن افترض أنها كافية، وإنّ تغيير حرف واحد من الكود البرمجي قد يُؤَدِي إلى دمار البرنامج بالكامل، نسيان فاصلة واحدة قد توقف المشروع بالكامل، وتغيير شيء واحد في سطر ما سيجعل البرنامج يعمل بطريقة سيئة تجعل العملية فاشلة برمتها، وهذا ونحن نتكلم عن برنامج بعدة أسطر، فما بالكم ببرنامج بألف سطر، أو مليون سطر؟ أو بلايين الأسطر المتداخلة.
كل خلية في الكائن الحي تحتوي في نواتها على الكود البرمجي لكل الكائن يمكن نقلها والقراءة منها، في جسم الإنسان في كل خلية يُوجد هذا الكود البرمجي بالكامل، ولو قمنا بمقارنة هذه الشيفرات الحيوية مع الشيفرات البرمجية سنرى مدى تعقيدها، وهناك من عمل على هذا الأمر كما في (شكل 31 عدد أسطر شيفرات الكائنات)، نلاحظ فيها أنّ الفأر يمتلك 120 مليون سطر برمجي في نواة كل خلية من خلاياه، وأنّ تغيير سطر واحد في البرنامج ينتج عنه أخطاء في البرنامج تؤدي إلى تلفه، وما حدث أبداً أنّ خطأً برمجياً في أحد البرامج أدى إلى حصول البرنامج على ميزة جديدة لم تكن موجودة فيه، مثلاً برنامج يقرأ ملفات صوتية، أمسى يقرأ ملفات صوتية وفيديو كليب بسبب خطأ ما، والخطأ في برنامج الحاسوب يساوي الطفرة في الكائنات الحية.
|
رابط 11 كم مليون سطر من الكود يستغرق الأمر |
ونلاحظ أنّ محرك الألعاب كراي انجين 2 يقارب في حجمه حجم البكتيريا، وكيرنال اللينكس القديم يحتوي على ضعف حجم البكتيريا |





اترك تعليقاً
يجب أنت تكون مسجل الدخول لتضيف تعليقاً.